
#Cdf to pdf pdf#
Notice, when the mean and standard deviations are equal, how the PDF correlates with the normal CDF in the section above.Īlso consider the difference between a continuous and discrete PDF. If we plot those possible values on the x-axis and plot the probability of measuring each specific value, x, or any value less than x on the y-axis, we will have the CDF of the random variable.
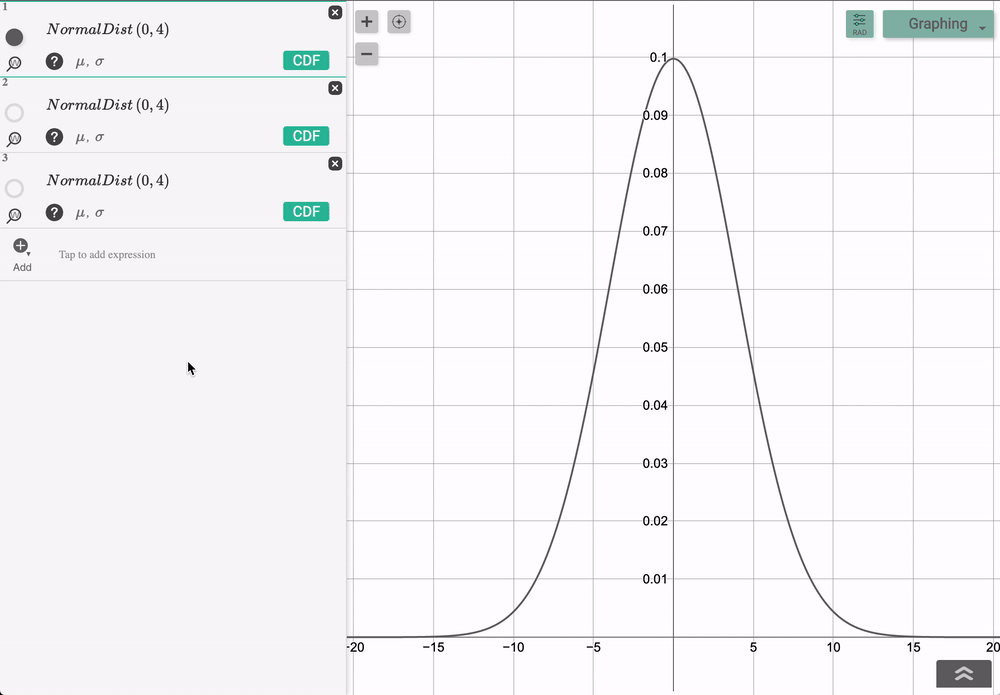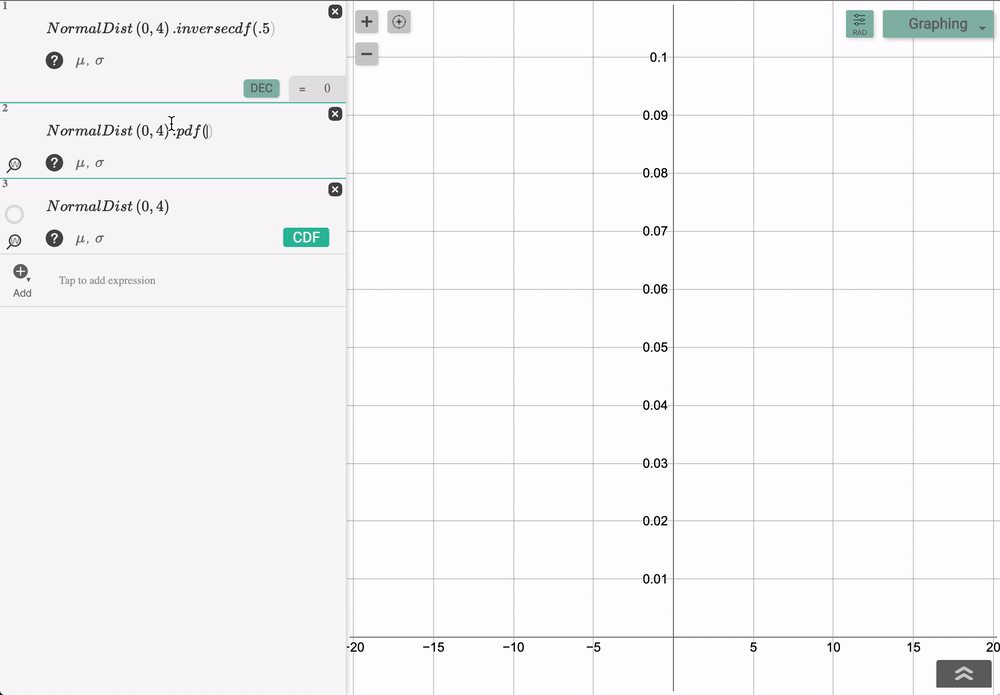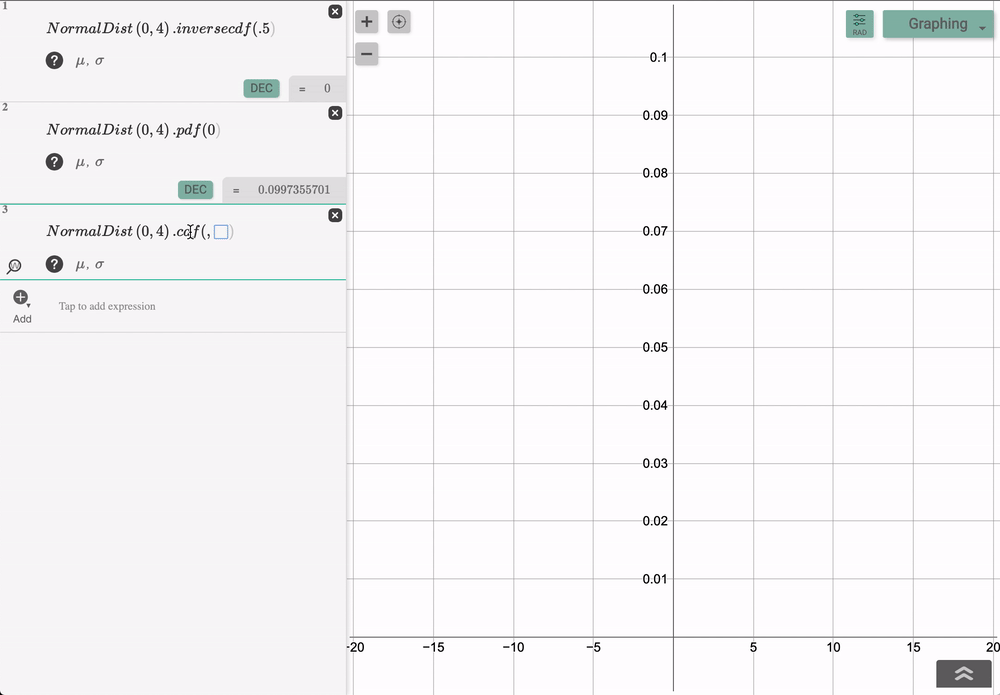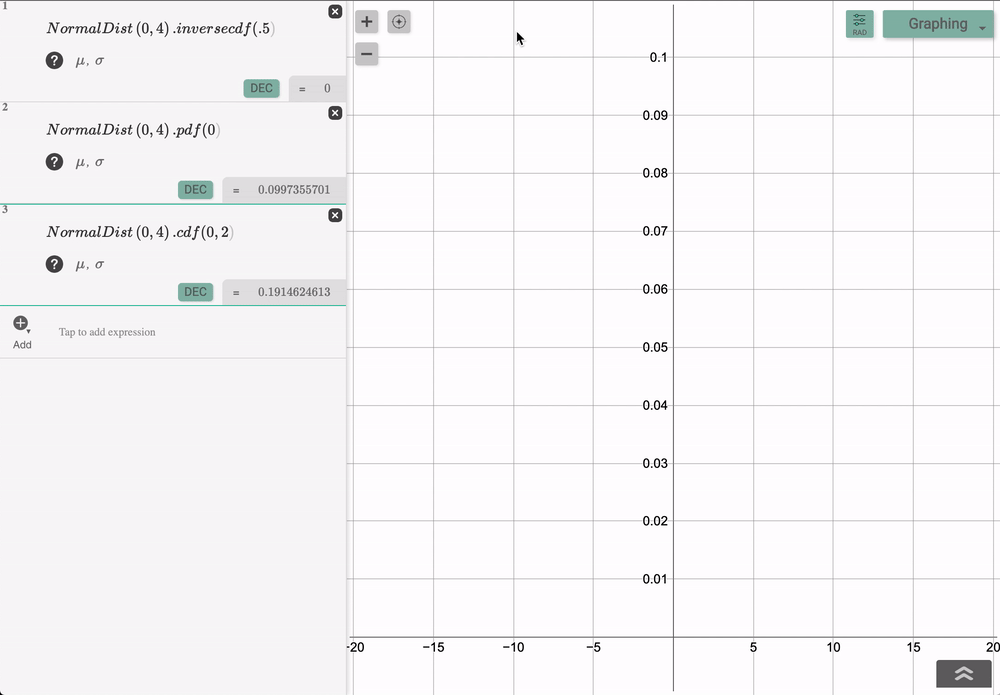
We would have a 1 in 6 chance of getting any of the possible values of the random variable (1, 2, 3, 4, 5, or 6). As CDFs are simpler to comprehend for both discrete and continuous random variables than PDFs, we will first explain CDFs.Ĭonsider tossing a fair 6-sidded dice. For those tasks we use probability density functions (PDF) and cumulative density functions (CDF).
#Cdf to pdf how to#
The question, of course, arises as to how to best mathematically describe (and visually display) random variables. In that way the random variable has a discrete component at x = 0 and continuous component where x > 0. For a possible example, though, you may be measuring a sample's weight and decide that any weight measured as a negative value will be given a value of 0. Such random variables are infrequently encountered. Mixed random variables have both discrete and continuous components. Other examples of continuous random variables would be the mass of stars in our galaxy, the pH of ocean waters, or the residence time of some analyte in a gas chromatograph. The coin could travel 1 cm, or 1.1 cm, or 1.11 cm, or on and on. That distance, x, would be a continuous random variable because it could take on a infinite number of values within the continuous range of real numbers. Other examples would be the possible results of a pregnancy test, or the number of students in a class room.īack to the coin toss, what if we wished to describe the distance between where our coin came to rest and where it first hit the ground. Such random variables can only take on discrete values. Such a function, x, would be an example of a discrete random variable. If we defined a variable, x, as the number of heads in a single toss, then x could possibly be 1 or 0, nothing else.
We could have heads or tails as possible outcomes. In the following sections these categories will be briefly discussed and examples will be given.Ĭonsider our coin toss again. As such there are three sorts of random variables: discrete, continuous and mixed. A random variable is simply a function that relates each possible physical outcome of a system to some unique, real number. In order to cope with this reality and to be able to describe the future states of a system in some useful way, we use random variables. Some outcomes truly are up in the air, unsettled until they are part of the past. Furthermore, it seems on exceedingly small scales that strict determinists are absolutely wrong there is no way to predict when, for example, a uranium atom will split, and if such an event affects the larger world then that macro event is truly unpredictable. If we knew all that, then we would know that particular coin toss had a 100% chance of landing the way it will land, and zero chance of any other outcome.īut we, of course, are often lacking even a mentionable fraction of such knowledge of the world. If we only knew the forces applied at a coin's toss, its exact distribution of mass, the various minute movements of air in the room. To a strict determinist, all such bets were settled long before any coin, metaphorical or not, was ever minted we simply do not yet know it. We care greatly to know what our chances are that we will get whirring turbines instead of a meltdown. Our coins may be, for example, various possible coolant flow rates or masses of uranium in a nuclear power plant. Heads or tails may even be a matter of life or death. But for others we have no choice but to hold judgment and speak in more vague terms, if we wish to say anything useful about the future at all.Īs scientists, it is, of course, our job to say something useful (or at the very least, authoritative.), while the metaphorical coins of important physical system are still in the air.
Will it land heads up? Tails? More than that, how long will it remain in the air? How many times will it bounce? How far from where it first hits the ground will it finally come to rest? For that matter, will it ever hit the ground? Ever come to rest?įor some such questions, we can and do settle on answers long before observations we are pretty sure gravity will hold and the coin will land. While it flips through space, what could you possibly say about its future? Say you were to take a coin from your pocket and toss it into the air.


 0 kommentar(er)
0 kommentar(er)
